Vectors Dot Product | Topic Playlist

Definition

The dot product of $\vec{a}$ and $\vec{b}$ is the sum of all multiplying all pairs of components in $\vec{a}$ and $\vec{b}$.

In two dimensional space using vector notation,

\begin{equation} \vec{a} \cdot \vec{b} = \langle a_{1},a_{2} \rangle \cdot \langle b_{1},b_{2} \rangle = a_{1}b_{1} + a_{2}b_{2} \end{equation}

In two dimensional space using matrix notation,

\begin{equation} \vec{a} \cdot \vec{b} = \begin{bmatrix} a_{1} \\ a_{2} \end{bmatrix}^{T} \begin{bmatrix} b_{1} \\ b_{2} \end{bmatrix} = \begin{bmatrix} a_{1} & a_{2} \end{bmatrix} \begin{bmatrix} b_{1} \\ b_{2} \end{bmatrix} = \begin{bmatrix} a_{1}b_{1} + a_{2}b_{2} \end{bmatrix} \end{equation}

In three dimensional space using vector notation,

\begin{equation} \vec{a} \cdot \vec{b} = \langle a_{1},a_{2},a_{3} \rangle \cdot \langle b_{1},b_{2},b_{3} \rangle = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3} \end{equation}

In three dimensional space using matrix notation,

\begin{equation} \vec{a} \cdot \vec{b} = \begin{bmatrix} a_{1} \\ a_{2} \\ a_{3} \end{bmatrix}^{T} \begin{bmatrix} b_{1} \\ b_{2} \\ b_{3} \end{bmatrix} = \begin{bmatrix} a_{1} & a_{2} & a_{3} \end{bmatrix} \begin{bmatrix} b_{1} \\ b_{2} \\ b_{3} \end{bmatrix} = \begin{bmatrix} a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3} \end{bmatrix} \end{equation}

Derivation of  $\vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|\cos(\theta)$

The dot product is used is because of the relationship,

\begin{equation} |\vec{a} - \vec{b}|^{2} = |\vec{a}||\vec{b}|\cos(\theta) \end{equation}

Where $0 \leq \theta \leq \pi$ is the angle formed by the vectors $\vec{a}$ and $\vec{b}$.

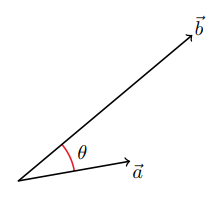
This can be proved in two dimensions using the Law of Cosines.

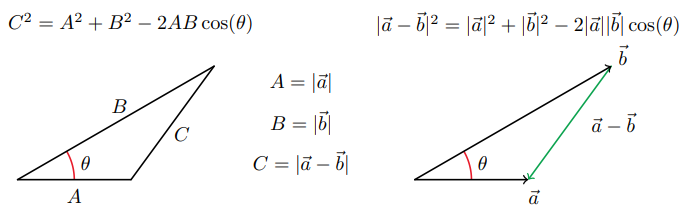
Starting with the Law of Cosines with the triangle side lengths as the lengths of vectors.

\begin{equation} |\vec{a} - \vec{b}|^{2} = |\vec{a}|^{2} + |\vec{b}|^{2} - 2|\vec{a}||\vec{b}|\cos(\theta) \end{equation}

Expand out some of the terms.

\begin{equation} |\langle a_{1}-b_{1},a_{2}-b_{2}\rangle|^{2} = \left(\sqrt{a_{1}^{2}+a_{2}^{2}}\right)^{2} + \left(\sqrt{b_{1}^{2}+b_{2}^{2}}\right)^{2} - 2|\vec{a}||\vec{b}|\cos(\theta) \end{equation} \begin{equation} (a_{1}-b_{1})^{2}+(a_{2}-b_{2})^{2} = a_{1}^{2}+a_{2}^{2} + b_{1}^{2}+b_{2}^{2} - 2|\vec{a}||\vec{b}|\cos(\theta) \end{equation} \begin{equation} a_{1}^{2}-2a_{1}b_{1}+b_{1}^{2}+a_{2}^{2}-2a_{2}b_{2}+b_{2}^{2} = a_{1}^{2}+a_{2}^{2} + b_{1}^{2}+b_{2}^{2} - 2|\vec{a}||\vec{b}|\cos(\theta) \end{equation}

Cancel out common terms.

\begin{equation} -2a_{1}b_{1}-2a_{2}b_{2} = - 2|\vec{a}||\vec{b}|\cos(\theta) \end{equation}

Divide both sides by $-2$.

\begin{equation} a_{1}b_{1} + a_{2}b_{2} = |\vec{a}||\vec{b}|\cos(\theta) \end{equation}

Finally, rewrite the LHS as the dot product.

\begin{equation} \vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|\cos(\theta) \end{equation}

To prove $\vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|\cos(\theta)$ in three or more dimensions, there are multiple ways, but one uses a change of basis to the plane containing $\vec{a}$ and $\vec{b}$ which reduces the problem to a two-dimensional space which was just proved.

Since $\vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|\cos(\theta)$, there are some easy tests to check if two vectors are orthogonal or pointing in the same direction, and pointing in opposite directions.

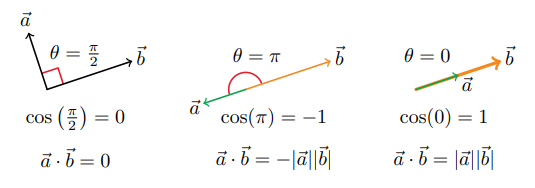
If $\vec{a}$ and $\vec{b}$ form a right angle with each other, called orthogonal, then the dot product is zero.

If $\vec{a}$ and $\vec{b}$ point in the same direction, then the dot product is $|\vec{a}||\vec{b}|$.

If $\vec{a}$ and $\vec{b}$ point in opposite directions, then the dot product is $-|\vec{a}||\vec{b}|$.

For two vectors $\vec{a}$ and $\vec{b}$, sometimes it's useful to find how much of a vector $\vec{b}$ is in the direction of $\vec{a}$. The scalar projection of $\vec{b}$ onto $\vec{a}$ is the length of the side of a right triangle with hypotenuse $\vec{b}$ and base in the direction of $\vec{a}$. It does not matter if $\vec{a}$ and $\vec{b}$ form an acute or obtuse angle. The projection will be exactly the same.

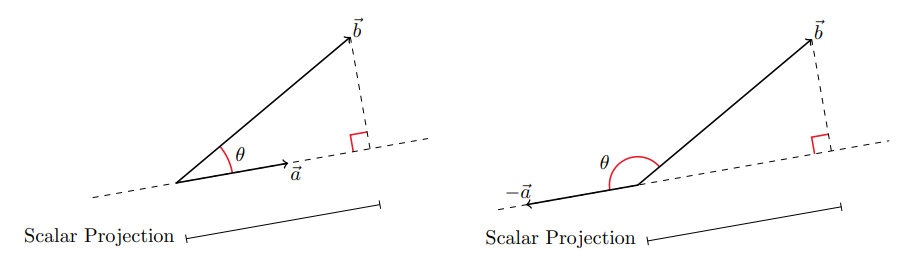
The dot product can be used to find the scalar projection $\vec{b}$ onto $\vec{a}$ because that length is $|\vec{b}|\cos(\theta)$.

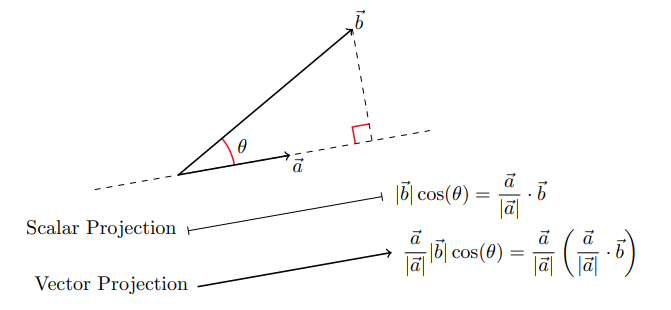
The vector projection of $\vec{b}$ onto $\vec{a}$ is a vector instead of a scalar. This can be calculated by multiplying the scalar projection by a length 1 vector, called a unit vector, in the direction of $\vec{a}$. Dividing $\vec{a}$ by its length will make a unit vector in the direction of $\vec{a}$.