Systems of Linear Equations | Chalkboard Video

Assuming there is a solution, solve the system of linear equations by setting different equations equal to each other and solving for the variables one at a time.

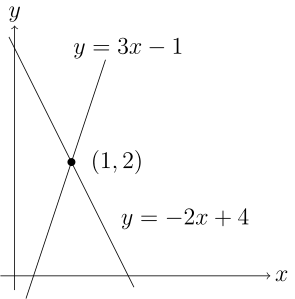
\begin{align} y &= 3x-1 \\ y &= -2x+4 \end{align} \begin{equation} 3x-1 = y = -2x+4 \end{equation}

Solving for $x$, then using the value for $x$ in either of the top two equations gives the solution as,

\begin{equation} (x,y) = (1,2) \end{equation}

Assuming there is a solution, solve the system of linear equations by setting different equations equal to each other and solving for the variables one at a time.

\begin{align} z &= 6-x-y \\ z &= 3+2x-y \\ z &= 8-x-2y \end{align}

Setting the first equation equal to the second equation,

\begin{equation} 6-x-y = z = 3+2x-y \end{equation}

Adding $y$ to each side leaves only $x$.

\begin{equation} 6-x = 3+2x \end{equation}

This equation has solution $x=1$.

Next, setting the first equation equal to the third equation to solve for $y$ and $z$,

\begin{equation} 6-x-y = 8-x-2y \end{equation}

The value of $x$ is known, so $y$ can be solved for.

\begin{equation} 6-1-y = 8-1-2y \end{equation}

This equation has solution $y=2$.

To solve for $z$, plug the values of $x$ and $y$ into any of the equation, giving the solution.

\begin{equation} (x,y,z) = (1,2,3) \end{equation}

The way these equations are written,

\begin{align} y &= 3x-1 \\ y &= -2x+4 \end{align}

Horizontal lines, like $y = 3$, but there's not a good way to represent vertical lines, like $x = -2$.

Writing the equations with all the variables on the LHS and the constant on the RHS fixes that limitation.

\begin{align} -3x + y &= -1 \\ 2x + y &= 4 \end{align}

The equations are also easier to solve in this form by directly adding equations to each other and storing the results in one of the equation rows.

\begin{equation} \text{Eqn }2 - \text{Eqn }1 \rightarrow \text{Eqn }2 \end{equation} \begin{align} -3x + y &= -1 \\ 5x + 0y &= 5 \end{align}

By adding the equations together to cancel out the $y$ term, solving for $x$ in the new $\text{Eqn }2$ is much easier. After finding $x$, the value for $x$ can be plugged into $\text{Eqn }1$ to solve for $y$.

Similarly to the previous example, the way these equations are written does not allow representing vertical planes where the coefficient on $z$ is $0$.

\begin{align} z &= 6-x-y \\ z &= 3+2x-y \\ z &= 8-x-2y \end{align}

Writing the equations with all the variables on the LHS and the constant on the RHS fixes that limitation.

\begin{align} x+y+z &= 6 \\ -2x+y+z &= 3 \\ x+2y+z &= 8 \end{align}

The idea is to add equations together to eliminate variables in other equations. This eliminates $x$ from the bottom two equations.

\begin{align} \text{Eqn }2 - 2(\text{Eqn }1) &\rightarrow \text{Eqn }2 \\ \text{Eqn }3 - \text{Eqn }1 &\rightarrow \text{Eqn }3 \end{align} \begin{align} x+y+z &= 6 \\ 0x+3y+3z &= 15 \\ 0x+1y+0z &= 2 \end{align}

It's less confusing, especially when working with even more equations and variables, to exchange rows sometimes.

\begin{equation} \text{Exchange Eqn }2 \text{ and Eqn }3 \end{equation} \begin{align} x+y+z &= 6 \\ 0x+1y+0z &= 2 \\ 0x+3y+3z &= 15 \end{align}

Now we can eliminate $y$ from the bottom equation.

\begin{equation} \text{Eqn }3 - 3(\text{Eqn }2) \rightarrow \text{Eqn }3 \end{equation} \begin{align} x+y+z &= 6 \\ 0x+1y+0z &= 2 \\ 0x+0y+3z &= 9 \end{align}

From here, the third equation can be solved, then the second (we didn't need the value of $z$ in this case), and then the first equation.

Working with systems of equations like this is a little clunky. A more convenient notation is augmented matrix equations, which is more compact, saves a lot of writing, and keeps things lined up.

For Example 1, the matrix equation and augmented matrix equations are,

\begin{align} -3x + y &= -1 \\ 2x + y &= 4 \end{align} \begin{equation} \begin{bmatrix} -3 & 1 \\ 2 & 1 \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} -1 \\ 4 \end{bmatrix} \end{equation} \begin{equation} \left[ \begin{matrix} -3 & 1 \\ 2 & 1 \end{matrix} \left| \begin{matrix} -1 \\ 4 \end{matrix} \right. \right] \end{equation}

The first and second row are the first and second equations. The first and second column is the coefficients on $x$ and $y$ in each equation, the right column is the RHS constants, and the vertical bar is like an equals sign. Very compact!

Now it's not so much writing to add rows together to eliminate variables.

\begin{equation} \left[ \begin{matrix} -3 & 1 \\ 2 & 1 \end{matrix} \left| \begin{matrix} -1 \\ 4 \end{matrix} \right. \right] \end{equation} \begin{equation} \frac{2}{3}R_{1}+R_{2} \rightarrow R_{2} \quad \left[ \begin{matrix} -3 & 1 \\ 0 & 5/3 \end{matrix} \left| \begin{matrix} -1 \\ 10/3 \end{matrix} \right. \right] \end{equation}

For Example 2, the augmented matrix equation can be solved fairly quickly.

\begin{align} x+y+z &= 6 \\ -2x+y+z &= 3 \\ x+2y+z &= 8 \end{align} \begin{equation} \begin{bmatrix} 1 & 1 & 1 \\ -2 & 1 & 1 \\ 1 & 2 & 1 \end{bmatrix}\begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 6 \\ 3 \\ 8 \end{bmatrix} \end{equation} \begin{equation} \left[ \begin{matrix} 1 & 1 & 1 \\ -2 & 1 & 1 \\ 1 & 2 & 1 \end{matrix} \left| \begin{matrix} 6 \\ 3 \\ 8 \end{matrix} \right. \right] \end{equation} \begin{equation} (-2)R_{1}+R_{2} \rightarrow R_{2} \quad \left[ \begin{matrix} 1 & 1 & 1 \\ 0 & -3 & -3 \\ 1 & 2 & 1 \end{matrix} \left| \begin{matrix} 6 \\ -15 \\ 8 \end{matrix} \right. \right] \end{equation} \begin{equation} (-1)R_{1}+R_{3} \rightarrow R_{3} \quad \left[ \begin{matrix} 1 & 1 & 1 \\ 0 & -3 & -3 \\ 0 & 1 & 0 \end{matrix} \left| \begin{matrix} 6 \\ -15 \\ 2 \end{matrix} \right. \right] \end{equation}