Divergence | Chalkboard Video

Two-dimensional vector field $\vec{F}(x,y)$

For a vector field $\vec{F}(x,y)$,

\begin{equation} \vec{F}(x,y) = \langle P(x,y),Q(x,y) \rangle \end{equation}

The divergence $\text{div}(\vec{F})$ is,

\begin{equation} \text{div}(\vec{F}) = \nabla \cdot \vec{F} = \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} \end{equation}

Three-dimensional vector field $\vec{F}(x,y,z)$

For a vector field $\vec{F}(x,y,z)$,

\begin{equation} \vec{F}(x,y,z) = \langle P(x,y,z),Q(x,y,z),R(x,y,z) \rangle \end{equation}

The divergence $\text{div}(\vec{F})$ is,

\begin{equation} \text{div}(\vec{F}) = \nabla \cdot \vec{F} = \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z} \end{equation}

The divergence at a point in a vector field $\vec{F}(x,y)$ is sort of the net amount of vector field arrows flowing out of that point, with arrows flowing out a positive contribution and arrows flowing in a negative contribution. It's not clear what that means, but the limit approximation actually makes a lot more sense.

If you want to find the divergence at a point $(x,y)$ in a vector field, it's approximately the flux of arrows flowing out of a small box around the point $(x,y)$. Here the box has width $\Delta x$ and height $\Delta y$. Since this is an approximation, we'll just use the vector field evaluated at the midpoint of each side. To calculate how much flux is flowing out of a side, take the dot product of the midpoint vector field arrow and unit normal vector $\vec{n}$ on that side times the length of that side.

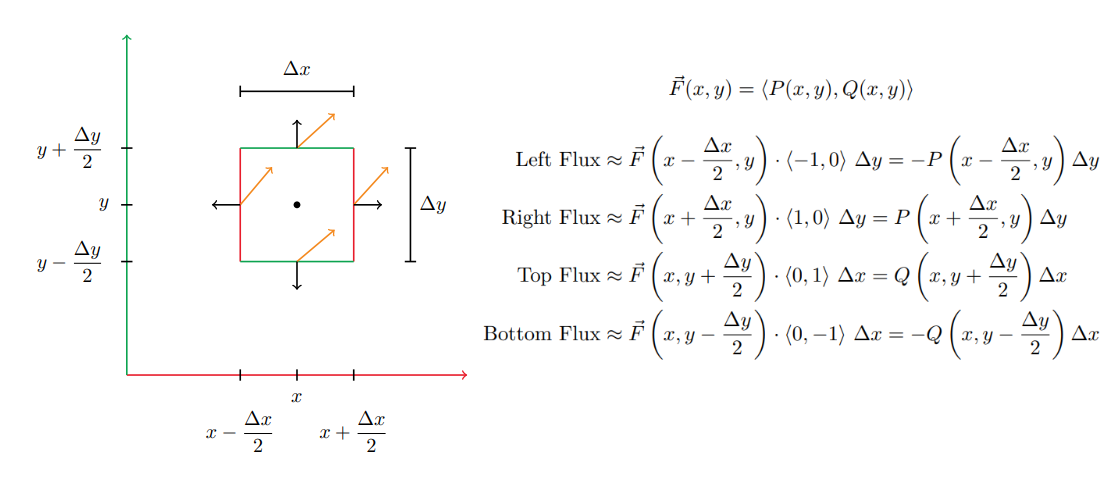
The total flux is the sum of all the side fluxes.

\begin{align} \text{Total Flux } &= \left[P\left(x+\frac{\Delta x}{2},y\right) - P\left(x-\frac{\Delta x}{2},y\right)\right] \Delta y \\ &+ \left[Q\left(x,y+\frac{\Delta y}{2}\right) - Q\left(x,y-\frac{\Delta y}{2}\right)\right]\Delta x \end{align}

There's still one piece missing though. In the limit as the box shrinks around the point $(x,y)$, the $\text{Total Flux}$ goes to zero because the side length go to zero.

\begin{equation} \lim_{\Delta x, \Delta y \rightarrow 0} \text{Total Flux } = 0 \end{equation}

So instead, the $\text{Total Flux}$ will be averaged over the area of the box, which is $\Delta x \Delta y$.

\begin{align} \nabla \cdot \vec{F}(x,y) &= \lim_{\Delta x, \Delta y \rightarrow 0} \frac{\text{Total Flux}}{\Delta x \Delta y} \\ &= \lim_{\Delta x \rightarrow 0} \frac{P\left(x+\frac{\Delta x}{2},y\right) - P\left(x-\frac{\Delta x}{2},y\right)}{\Delta x} \\ &+ \lim_{\Delta y \rightarrow 0} \frac{Q\left(x,y+\frac{\Delta y}{2}\right) - Q\left(x,y-\frac{\Delta y}{2}\right)}{\Delta y} \end{align}

This isn't usually the way they are written, but these are the partial derivatives of $P$ and $Q$ with respect to $x$ and $y$.

\begin{align} \frac{\partial P}{\partial x} &= \lim_{\Delta x \rightarrow 0} \frac{P\left(x+\frac{\Delta x}{2},y\right) - P\left(x-\frac{\Delta x}{2},y\right)}{\Delta x} \\ \frac{\partial Q}{\partial y} &= \lim_{\Delta y \rightarrow 0} \frac{Q\left(x,y+\frac{\Delta y}{2}\right) - Q\left(x,y-\frac{\Delta y}{2}\right)}{\Delta y} \end{align}

It's usually written as $P(x + \Delta x,y) - P(x,y)$ and $Q(x,y + \Delta y) - Q(x,y)$, but they still have a difference of $\Delta x$ and $\Delta y$ in their input arguments.

So then the flux going out of the box averaged over the area of the box in the limit as the box shrinks to a point is,

\begin{equation} \nabla \cdot \vec{F}(x,y) = \lim_{\Delta x, \Delta y \rightarrow 0} \frac{\text{Total Flux}}{\Delta x \Delta y} = \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} \end{equation}

The idea for divergence of a vector field in 3D is similar to 2D. There's now a cube centered around a point $(x,y,z)$ with width $\Delta x$, length $\Delta y$, and height $\Delta z$.

There are six sides of the cube to calculate the flux for. To calculate how much flux is flowing out of a side, take the dot product of the midpoint vector field arrow and unit normal vector $\vec{n}$ on that side times the area of that side.

\begin{equation} \vec{F}(x,y,z) = \langle P(x,y,z),Q(x,y,z),R(x,y,z)\rangle \end{equation} \begin{align} \text{Left Flux} &\approx \vec{F}\left(x-\frac{\Delta x}{2},y,z\right) \cdot \langle -1,0,0 \rangle ~\Delta y \Delta z = -P\left(x-\frac{\Delta x}{2},y,z\right) \Delta y \Delta z \\ \text{Right Flux} &\approx \vec{F}\left(x+\frac{\Delta x}{2},y,z\right) \cdot \langle 1,0,0 \rangle ~\Delta y \Delta z = P\left(x+\frac{\Delta x}{2},y,z\right) \Delta y \Delta z \\ \text{Front Flux} &\approx \vec{F}\left(x,y+\frac{\Delta y}{2},z\right) \cdot \langle 0,1,0 \rangle ~\Delta x \Delta z = Q\left(x,y+\frac{\Delta y}{2},z\right) \Delta x \Delta z \\ \text{Back Flux} &\approx \vec{F}\left(x,y-\frac{\Delta y}{2},z\right) \cdot \langle 0,-1,0 \rangle ~\Delta x \Delta z = -Q\left(x,y-\frac{\Delta y}{2},z\right) \Delta x \Delta z \\ \text{Top Flux} &\approx \vec{F}\left(x,y,z+\frac{\Delta z}{2}\right) \cdot \langle 0,0,1 \rangle ~\Delta x \Delta y = R\left(x,y,z+\frac{\Delta z}{2}\right) \Delta x \Delta y \\ \text{Bottom Flux} &\approx \vec{F}\left(x,y,z-\frac{\Delta z}{2}\right) \cdot \langle 0,0,-1 \rangle ~\Delta x \Delta y = -R\left(x,y,z-\frac{\Delta z}{2}\right) \Delta x \Delta y \end{align}

The divergence at $(x,y,z)$ is the limit of the sum of all the fluxes divided by the volume of the cube as the cube shrinks to the point.

\begin{align} \frac{\text{Total Flux}}{\text{Volume}} &= \frac{\text{Right Flux } + \text{Left Flux}}{\Delta x \Delta y \Delta z} \\ &+ \frac{\text{Back Flux } + \text{Front Flux}}{\Delta x \Delta y \Delta z} \\ &+ \frac{\text{Top Flux } + \text{Bottom Flux}}{\Delta x \Delta y \Delta z} \\ \end{align} \begin{align} \nabla \cdot \vec{F} &= \lim_{\Delta x, \Delta y, \Delta z \rightarrow 0} \frac{\text{Total Flux}}{\text{Volume}} \\ &= \lim_{\Delta x \rightarrow 0} \frac{P\left(x+\frac{\Delta x}{2},y,z\right) - P\left(x-\frac{\Delta x}{2},y,z\right)}{\Delta x} \\ &+ \lim_{\Delta y \rightarrow 0} \frac{Q\left(x,y+\frac{\Delta y}{2},z\right) - Q\left(x,y-\frac{\Delta y}{2},z\right)}{\Delta y} \\ &+ \lim_{\Delta z \rightarrow 0} \frac{R\left(x,y,z+\frac{\Delta z}{2}\right) - R\left(x,y,z-\frac{\Delta z}{2}\right)}{\Delta z} \end{align}

The limits are the partial derivatives of $P$, $Q$, and $R$ with respect to $x$, $y$, and $z$. That means the divergence is,

\begin{equation} \nabla \cdot \vec{F} = \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z} \end{equation}