Courses

1. Linear Algebra
2. Multivariable Calculus
3. Differential Equations
4. Miscellaneous Topics

Differential Equations

1. Introduction
   1. Notation and Definitions
   2. Verifying Solutions
   3. Initial Values Problems
2. First Order Differential Equations
   1. Direction Fields
   2. Equilibria, Stability, and Phase Lines
   3. Separable Equations
   4. Integrating Factor
   5. Bernoulli Equations and Substitutions
   6. Exact Equations
   7. Exact Equations with Integrating Factor
   8. Euler's Method
   9. Existence and Uniqueness
   10. Interval of Validity
   11. Applications
       1. Radioactive Decay and Population Growth
       2. Mixing Tank Problem
       3. Terminal Velocity
       4. Continuous Compound Interest
3. Wrońskian
4. Second Order Differential Equations
   1. $ay''+by'+cy = 0$
      1. Distinct Real Roots
      2. Repeated Real Root
      3. Imaginary Roots
   2. Spring-Mass-Damper
      1. Equivalent RLC Circuit
      2. Underdamped, Overdamped, Critically Damped
      3. Undamped Oscillations and Resonance
   3. Method of Undetermined Coefficients
   4. Reduction of Order
   5. Variation of Parameters
   6. Cauchy-Euler Equations
5. Laplace Transform
   1. Lookup Table and WolframAlpha
6. Systems of ODEs
   1. Simplest Case $\begin{bmatrix}x' \\ y'\end{bmatrix} = \begin{bmatrix}a & b \\ c & d \end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix}$
      1. Poincaré Diagram
7. Preview of Dynamical Systems
   1. Self-Study
   2. Rössler Attractor

Additional Resources

1. WolframAlpha Examples
2. Direction Field Plotter by Ariel Barton
3. Phase Plane Plotter by Ariel Barton

Poincaré Diagram | Topic Playlist

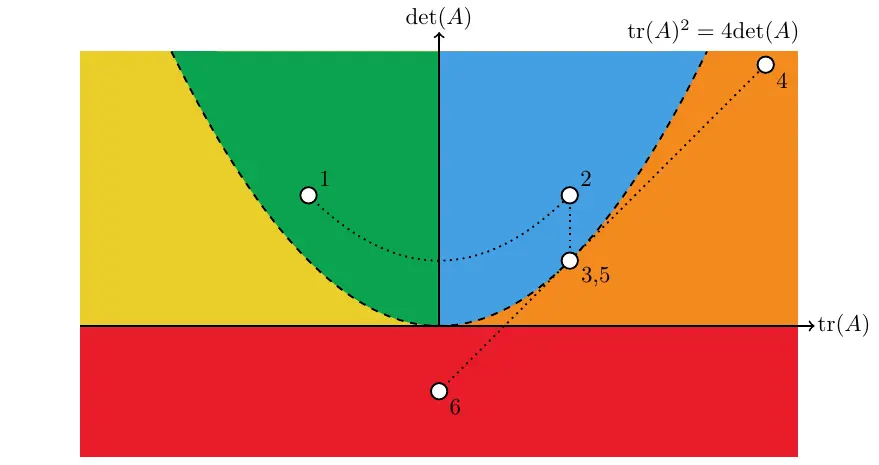
The solution of a two dimensional system of linear, constant coefficient, homogeneous differential equations can be classified using the trace and the determinant of the coefficient matrix. A plot of the trace and determinant has regions where certain solutions types occur, such as saddles and spirals. The diagram is called a Poincaré Diagram, mapping the four-dimensional space of all 2x2 matrices to a two-dimensional space.

Region Solution Types | Explanation Video

There are only so many types of solutions that can occur in a two dimensional system of linear, constant coefficient, homogeneous differential equations. The solution type is determined by the eigenvalues, and whether or not there's a complete set of eigenvectors in the repeated eigenvalue case.

\begin{equation} \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} \qquad A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \end{equation}

The trace and determinant of the constant coefficient matrix and their relationship to the eigenvalues,

\begin{equation} \text{det}(A) = ad-bc=\lambda_{1}\lambda_{2} \qquad \text{tr}(A) = a+d=\lambda_{1}+\lambda_{2} \end{equation}

are a convenient tool to classify the solution type just from just the 2x2 matrix elements.

Click the image for higher resolution.

Traversing the Phase Portraits | Animiation

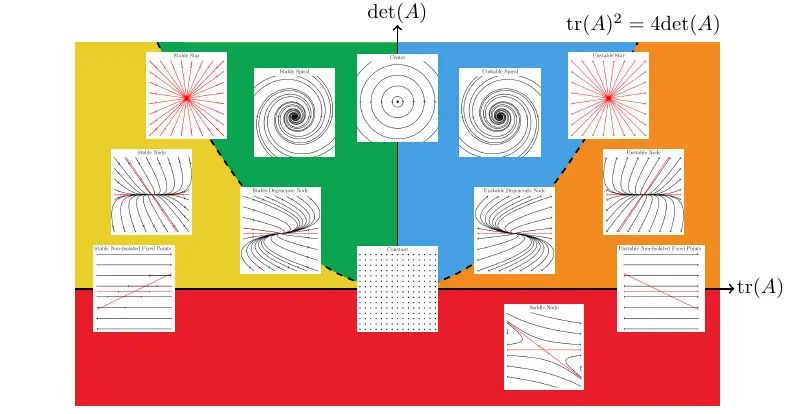
By changing the elements of the coefficient matrix,

\begin{equation} \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} \end{equation}

the phase portraits will deform. As the trace and determinant cross through a boundary separating types of solutions, the phase portraits will transition from one solution type to another.

Clicking on the image or the YouTube link above will show an animation of passing through several boundaries and how the phase portrait transforms from one solution type to another while crossing through each boundary.