Table of Contents
Differential Equations
channel logo

Courses

  1. Linear Algebra
  2. Multivariable Calculus
  3. Differential Equations
  4. Miscellaneous Topics

Differential Equations

  1. Introduction
    1. Notation and Definitions
    2. Verifying Solutions
    3. Initial Values Problems
  2. First Order Differential Equations
    1. Direction Fields
    2. Equilibria, Stability, and Phase Lines
    3. Separable Equations
    4. Integrating Factor
    5. Bernoulli Equations and Substitutions
    6. Exact Equations
    7. Exact Equations with Integrating Factor
    8. Euler's Method
    9. Existence and Uniqueness
    10. Interval of Validity
    11. Applications
      1. Radioactive Decay and Population Growth
      2. Mixing Tank Problem
      3. Terminal Velocity
      4. Continuous Compound Interest
  3. Wrońskian
  4. Second Order Differential Equations
    1. $ay''+by'+cy = 0$
      1. Distinct Real Roots
      2. Repeated Real Root
      3. Imaginary Roots
    2. Spring-Mass-Damper
      1. Equivalent RLC Circuit
      2. Underdamped, Overdamped, Critically Damped
      3. Undamped Oscillations and Resonance
    3. Method of Undetermined Coefficients
    4. Reduction of Order
    5. Variation of Parameters
    6. Cauchy-Euler Equations
  5. Laplace Transform
    1. Lookup Table and WolframAlpha
  6. Systems of ODEs
    1. Simplest Case $\begin{bmatrix}x' \\ y'\end{bmatrix} = \begin{bmatrix}a & b \\ c & d \end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix}$
      1. Poincaré Diagram
  7. Preview of Dynamical Systems
    1. Self-Study
    2. Rössler Attractor

Additional Resources

  1. WolframAlpha Examples
  2. Direction Field Plotter by Ariel Barton
  3. Phase Plane Plotter by Ariel Barton


NARROW DISPLAY WARNING

You are most likely using a tablet or mobile device in portrait orientation. This website is best viewed using a typical computer screen with the browser window maximized.

Viewing this website in portrait orientation can cause problems with equations being longer than the screen width (you can scroll to the right), images being poorly sized, and the font size of maths text being much smaller than regular text. If your only option is a tablet or mobile device, your viewing experience will be better if you view this website in landscape orientation. You might need to refresh the page to fix any problems after rotating.

Rössler Attractor | youtube icon Topic Playlist

3D Print your own model

For those who would like to purchase their own 3D printed Rössler attractor, there are companies that will give a quote to 3D print an STL file you provide. I was able to find an STL file you can use on Thingiverse. There are a few models there, but one of them looks extremely similar to the physical model pictured below. (In fact, I wouldn't be surprised if that exact STL file was used since I found very few relevant search results.) That model fits in a 15cm cube.

Definition

The system of equations for the Rössler Attractor has three parameters and only one nonlinear term.

\begin{align} \frac{\text{d}x}{\text{d}t} &= -y-z \\ \frac{\text{d}y}{\text{d}t} &= x+ay \\ \frac{\text{d}z}{\text{d}t} &= b+z(x-c) \end{align}

There are multiple values of the parameters that form a strange attractor, but the case when $a=0.2$, $b=0.2$, and $c=5.7$ has been studied by Rössler and many others.

Period-Doubling Bifurcations

The system undergoes period-doubling bifurcations when changing the parameters, leading to chaos. YouTubeyoutube icon Video

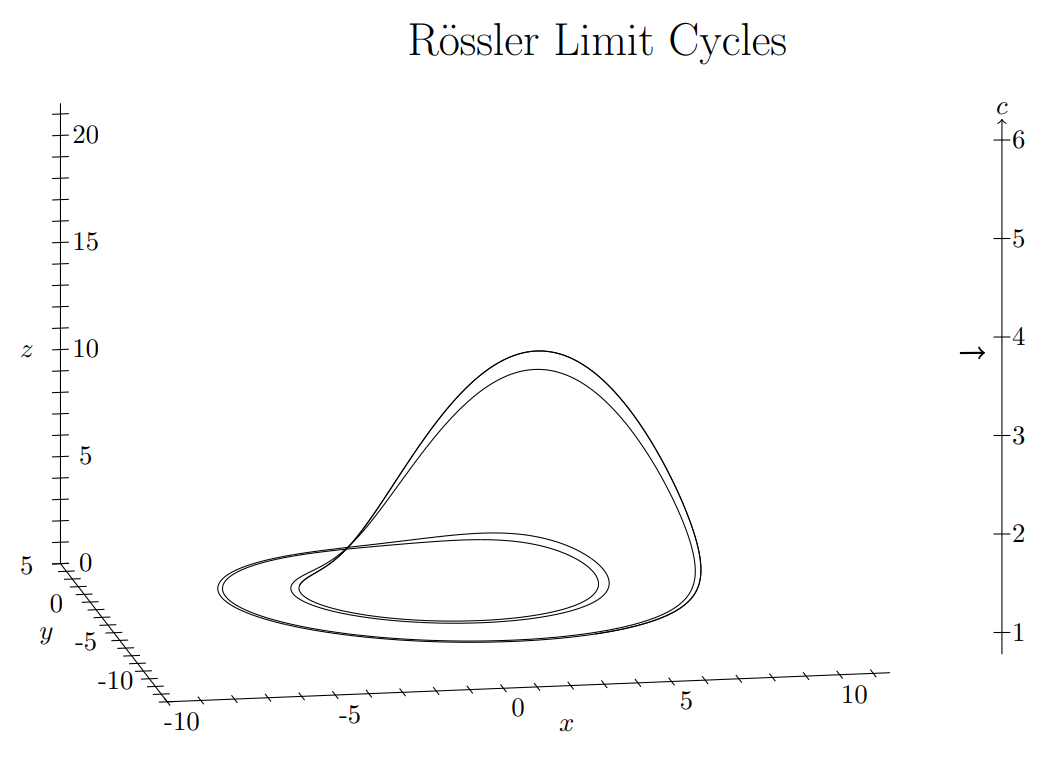
rossler period doubling

Where to learn more?

This is a very small portion of all the interesting behaviours of the Rössler system. There are ways to apply iteration maps, bifurcations diagrams, fractals, and many other concepts from dynamical systems theory. There would generally be covered in an introductory dynamical systems course.